Does K&n Air Filter Increase Horsepower

How Does yard-Means Clustering in Machine Learning Work?

One of the near famous topics under the realm of Unsupervised Learning in Machine Learning is k-Means Clustering. Even though this clustering algorithm is fairly simple, it can look challenging to newcomers into the field. In this mail, I try to tackle the process of k-Means Clustering with two different examples. The first example will focus more on the large picture and visualizing the process, while the 2nd example focuses on the underlying calculation involved.

Unsupervised Learning and Clustering

The primary difference between Supervised and Unsupervised learning algorithms is the absence of data labels in the latter. With unsupervised learning, data features are fed into the learning algorithm, which determines how to label them (usually with numbers 0,1,two..) and based on what. This "based on what" part dictates which unsupervised learning algorithm to follow.

Most unsupervised learning-based applications utilise the sub-field called Clustering. Clustering is the process of grouping data samples together into clusters based on a certain feature that they share — exactly the purpose of unsupervised learning in the starting time place.

Then, what is k-Means, and why would nosotros use it?

Being a clustering algorithm, k-Means takes information points as input and groups them into k clusters. This process of group is the grooming phase of the learning algorithm. The result would be a model that takes a data sample as input and returns the cluster that the new data point belongs to, co-ordinate the training that the model went through. How can this be useful? Well, that's how content promotion and recommendation usually works — in a very simplistic way. Websites may cull to put people in bubbles (i.e. clusters) with other people who share similar activities (i.east. features) on the website. This way, the recommended content will be somewhat on-point, as existing users with similar activities are likely to be interested in like content. Moreover, every bit a new person goes into the ecosystem of the website, that person will be placed within a particular cluster, and the content recommendation organisation takes care of the rest.

Edifice on that idea, thousand-Ways is only a clustering algorithm. It uses the distance betwixt points as a measure out of similarity, based on one thousand averages (i.e. ways). This is a very interesting algorithm, and then allow's get downward to business.

Putting the k in k-Means

The idea behind grand-Means is that, we want to add thou new points to the data nosotros accept. Each one of those points — chosen a Centroid — will exist going effectually trying to center itself in the center of i of the grand clusters we have. Once those points stop moving, our clustering algorithm stops.

Equally you lot might've suspected, the value of grand is of nifty importance. This k is called a hyper-parameter; a variable whose value we set before training. This k specifies the number of clusters we desire the algorithm to yield. This number of clusters is actually the number of centroids going around in the information.

Before nosotros go further, let'due south take a expect at how everything then far fits within the big motion picture:

Nosotros know that the core of Auto Learning lies on the thought of generalization — making a reliable prediction of outputs for inputs that the model has never seen earlier.
Unsupervised Learning is all virtually grouping data samples together, regardless of their labels (if they accept whatsoever).
Clustering is an Unsupervised Learning algorithm that groups data samples into thousand clusters.
The algorithm yields the k clusters based on k averages of points (i.eastward. centroids) that roam effectually the data fix trying to center themselves — one in the center of each cluster.

g-Means: in cursory

What is a better summary of an algorithm than pseudo-code?

                Assign initial values for each                  u                  (from                  u=i till                  u=grand);                Repeat {
                  Assign each point in the input data to the                  u                  that is closest
                  to information technology in value;                Calculate the new mean for each                  u;                if all                  u                  values are unchanged { break out of loop; }
}

m-Means: in particular

If you've read any of my posts before, you lot probably know that I similar to explain with an example first and then talk near the technical aspect of our topic. Moreover, I don't similar to walk the reader through the overwhelming mathematics behind topics, equally I believe those are more of import to researchers than to people who have a cocky-interest in the matter.

Back to k-Means and our first case. Allow's say nosotros take a data set that looks similar the following figure when plotted out:

To u.s.a. humans, this information looks similar it perfectly fits within three groups (i.eastward. clusters). However, machines tin't see that, every bit those points are actual data "points" whose values are just numbers that cannot be sensible to the motorcar.

Referring to the objective of clustering, we have a set up of unlabeled data points that we desire to put in groups. Those groups are usually labeled with numbers (0,1,2..) by the algorithm itself. Implicitly, what we really need is actually a decision boundary that separates the groups. Why? In practice, inference works by associating a data point with a respective cluster. That's where the decision boundary appears to be important.

k-Means clustering is all about putting the training points we have into clusters. But the purpose of it follows the aforementioned idea. Nosotros want to know which data points vest together without having any labels for whatever of them.

We start the algorithm by placing one thousand unlike averages (i.e. means) whose values are either initialized randomly or set to real data points on the plane. Let'southward get-go with k=three, as the information "seems" to be falling into three groups (we volition get dorsum to this "seems" word after in the post). For explanation-related purposes, lets randomly initialize the values (i.e. positions) of the averages:

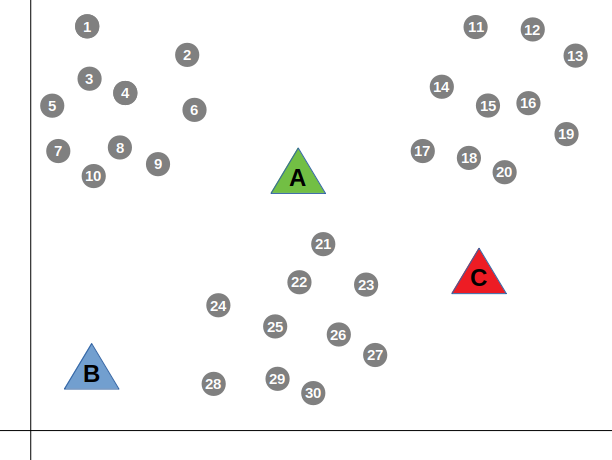
Now, the algorithm goes through the data points i-past-one, measuring the distance between each bespeak and the three centroids (A, B and C). The algorithm then groups the the data point with the closest centroid (i.eastward. closest in distance).

For instance, data point number 21 volition vest to group A in the green color, merely considering it'south closer in altitude to centroid A:

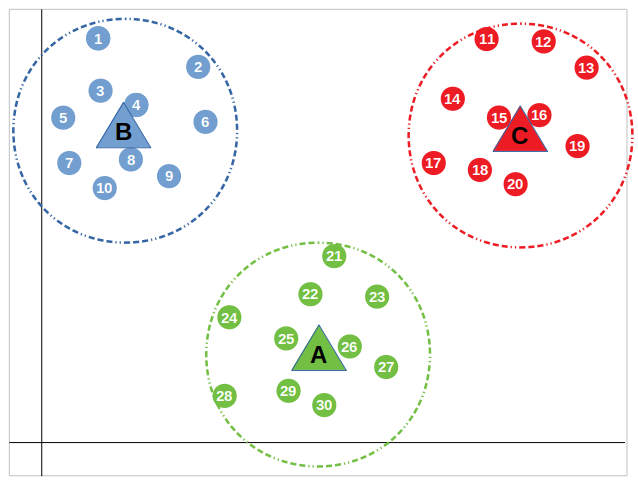
Every bit soon as we're washed associating each information betoken with its closest centroid, nosotros re-calculate the means — the values of the centroids; the new value of a centroid is the sum of all the points belonging to that centroid divided by the number of points in the group.

We continue doing the above until no centroid changes its value in re-adding. This ways that each centroid has centered itself in the heart of its cluster, which is surrounded by its own circular determination boundary:

Some other Example

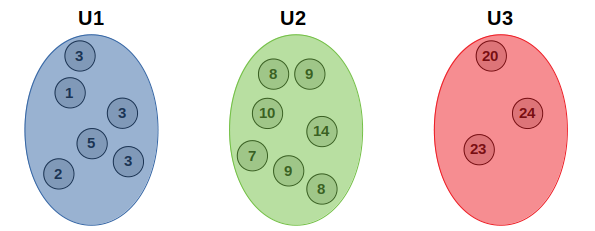
Allow's take another example, but from a different perspective this fourth dimension. Let's say nosotros have the post-obit set of points that we want to cluster into 3 groups:

This information is not put in a visually-appealing manner. We just have a set of points that we want to cluster. Some other of import note is that the values in the circles symbolizing those data points are bodily values of the points. They're not put a fashion of showing the sequence of data like our previous example. Rather, these values are a quantification of some feature value F. I put them this way to make it easier on you to understand how the calculation of ways works.

Let'south prepare our empty clusters:

Call back of these clusters as but numberless that will incorporate points from our information set.

Let's initialize the U values (i.e. means/centroids) to:

                U1 = six
U2 = 12
U3 = xviii

These values can be random, but for simplicity reasons, they were called to be uniformly scattered along the data space (1 through 24).

Since we already have our ways, we can kickoff calculating distances betwixt any point whose feature F value is F and the three means (U1, U2 & U3), where the absolute altitude follows:

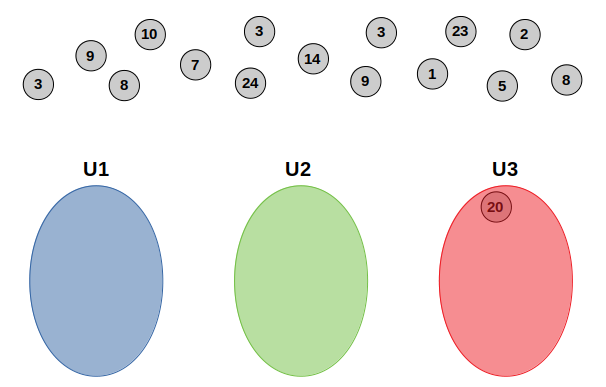
                altitude = | F - U |

For starters, let's have the data point whose feature F value is twenty:

                |xx - U1| = |20 - 6| = xiv
|20 - U2| = |20 - 12| = 8
|20 - U3| = |twenty - 18| = 2

According to the above calculations, the data betoken whose value is 20 is closer in distance to hateful U3. Therefore, we "characterization" the point every bit U3 past putting it in its corresponding cluster/bag:

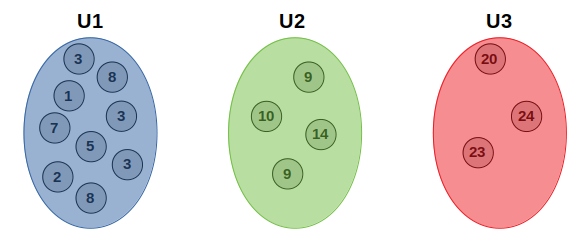
And the aforementioned goes for all the other points:

                |iii - U1| = |20 - 6| = 3
|3 - U2| = |twenty - 12| = 9
|3 - U3| = |20 - 18| = fifteen

And so on, until we have all our data points in their advisable clusters:

Post-obit the algorithm, we now need to re-summate the means (U1, U2 too every bit U3):

                U1 = (iii+8+1+iii+7+five+two+3+eight) / 9 = 4.44
U2 = (9+10+xiv+ix) / 4 = ten.5
U3 = (20+24+23) / 3 = 22.33

Upon the beginning of our execution, our U values were vi, 12, and 18, respectively. Now, after the showtime iteration, the values became 4.44, 10.v and 22.33, respectively. We now accept to get through the distance calculation step again, but with the new hateful values. We empty out our bags/clusters, and outset again:

Let'due south start with a random point this time, say, the point whose feature F value is eight. The distance calculations would follow:

                |8 - U1| = |8 - four.44| = 3.56
|viii - U2| = |eight - x.five| = 2.v
|8 - U3| = |viii - 22.33| = fourteen.33

So, the data point with the value 8 belongs to the cluster of mean value U2, as it's is closest to it in distance. If you lot still retrieve, the same data point (8) belonged to U1 in the first run. This makes it evident how important the mean values are.

Running the algorithm over and over once again until the hateful values don't alter upon calculation will reach the post-obit germination, with mean values two.83, 9.29 and 22.33, respectively:

Final Notes

Equally yous've seen in our 2nd example, the mean values nosotros operate with at any given indicate are of keen importance to the reliability of the model. This does not exclude the initial values. In fact, with really bad starting positions, the algorithm could get the clustering completely wrong! Therefore, some other initialization approach would be to choose our initial k positions from the data set itself, setting one of the points as a hateful value in its ain environs. Either manner, it is common practice to run the algorithm on the same data set repeatedly until we observe a most common solution and clustering formation — and we stick to it.

Remember the stage at which nosotros said that data "seems" to have been partitioned into three? Well, that was only to testify the importance of the human middle in such applications. Since we don't have a ground truth error estimation (equally it normally requires labels), we demand another measure for the hyper-parameters. For a lot of applications, a person looking at the plot and determining the grand value is sufficient. However, this does not overestimate the importance of the thou value in any way.

Finally, one of the apparent strengths of k-Means is the fact that it gives an average value of the feature over the cluster, not only the cluster itself. This could be very useful in segmentation-related image processing tasks — when dealing with division as a clustering problem.